
विद्युत क्षेत्र / Electric Field
किसी आवेश के चारों तरफ का वह क्षेत्र जिसमें उसका प्रभाव किसी अन्य आवेश द्वारा अनुभव किया जा सके विद्युत क्षेत्र कहलाता है।
या
किसी आवेश अथवा आवेशों के निकाय के चारों तरफ वह क्षेत्र (स्थान) जिसमें रखा अन्य आवेश आकर्षण या प्रतिकर्षण बल अनुभव करे विद्युत क्षेत्र कहलाता है। विद्युत क्षेत्र का विचार माइकल फैराडे ने दिया था, जिसमें कोई भी q आवेश से आवेशित कण विद्युत बल F का अनुभव करता है, जिसका मान F = qE होता है।
अतः किसी स्थान पर विद्युत क्षेत्र का मान $$ E = \frac{F}{q} ——-(1) $$ से दिया जाता है।
विद्युत क्षेत्र की तीव्रता (Intensity of Electric Field) :—
विद्युत क्षेत्र के किसी बिन्दु पर क्षेत्र की तीव्रता वहाँ रखे हुए परीक्षण मात्रक धन आवेश पर लगने वाले बल के बराबर होती है। बल की दिशा ही क्षेत्र की दिशा होती है। इस विद्युत क्षेत्र को E से प्रदर्शित करते हैं।
किसी विद्युत क्षेत्र E में qo परीक्षण आवेश रखने पर उस पर लगने वाला बल
F = qoE
या
$$ E = \frac{F}{q_0} $$
ध्यान रहे कि यहाँ qo का मान इतना कम होना चाहिए कि इसके कारण विद्युत क्षेत्र की तीव्रता परिवर्तित नहीं हो।
कार्यरत बल की दिशा एकांक धन आवेश पर लगने वाले बल विद्युत क्षेत्र की तीव्रता एक सदिश राशि है जिसकी दिशा के अनुदिश होती है। इसकी इकाई न्यूटन/कूलॉम तथा विमा [MLT-3A-1] है।
वैद्युत क्षेत्र में किसी आवेश पर लगने वाला बल – [ बल = वो आवेश x वहाँ का वैद्युत क्षेत्र ]
F = q0E ——- (2) [ ∵ F = ma]
ma = q0E
$$ a = \frac{q_0E}{m} $$
समीकरण (3) परीक्षण आवेश के त्वरण को व्यक्त करता है |
एकल आवेश का वैद्युत क्षेत्र (विलगित आवेश का वैद्युत क्षेत्र ) :-
Q आवेश के कारण r दूरी पर उत्पन्न वैद्युत क्षेत्र ज्ञात करना :-
Q•—— r ——-•q0
वैद्युत क्षेत्र = $$ E = \frac{F}{q_0} —– 3 $$
कुलॉम बल से $$ F = \frac{KQq_0}{r^2}$$
F का मान समीकरण (3) में रखने पर
$$ E = \frac{KQq_0}{r^2 q_0}$$
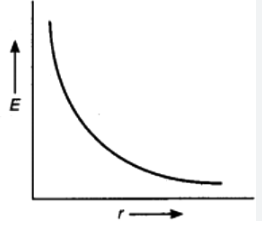
$$ E = \frac{KQ}{r^2}$$
$$ [∵ K = \frac{1}{4 \pi \varepsilon_0}] $$
$$ [∵ K = \frac{Q}{4 \pi \varepsilon_0 r^2}] $$
वैद्युत क्षेत्र की दूरी पर निर्भरता $$ E \ $$
Post Views: 128